0715 · Prove trig identity (1/(sin^2 x))(sin^2 x/cos^2 x) 1 = = (sin^2 x sin^2 xcos^2 x)/(sin^2 xcos^2 x) = ((sin^2 x)(1 cos^2 x))/(sin^2xcos^2 x) = =sin^2x/cos^2 x = tan^2 x Trigonometry ScienceSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreHere I give proofs of two Pythagorean trigonometric identities you should knowsin divided by cos equals tan and sin squared plus cos squared equals 1YOUTUB

Lesson 4 5 Double Angle Formulas
Trig identities tan^2x
Trig identities tan^2x-Math2org Math Tables Trigonometric Identities sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x)Sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) cos x cos y = 2 sin ( (x y)/2 ) sin ( (x y)/2 ) Trig Table of Common Angles angle



Solved 17 Prove The Following Trig Identities Tan 2x Chegg Com
· This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Confirming that the result is an identity Yes, sec2 − 1 = tan2x is an identity · In this section we look at how to integrate a variety of products of trigonometric functions These integrals are called trigonometric integralsThey are an important part of the integration technique called trigonometric substitution, which is featured in Trigonometric SubstitutionThis technique allows us to convert algebraic expressions that we may not be ableIdentities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan x equation 5 sin 2 x cos 2 x = 1 equation 6 tan 2 x 1 = sec 2 x equation 7 1 cot 2 x = csc 2 x equation 8 cos (x y) = cos x cos y sin x sin y equation 9 sin (x y) = sin x cos y cos x sin y equation 10 cos (x) = cos x equation 11
I need to prove this identity tan^2xsin^2x = tan^2xsin^2x start with left side tan^2xsin^2x =(sin^2x/cos^2x)sin^2x =(sin^2xsin^2xcos^2x)/cos^2x =sin^2x(1cos^2x)/cos^2x =sin^2x*sin^2x/cos^2x =tan^2xsin^2xUsing the sum and difference formula for trigonometric identities, we get \( \sin {x}\cos {y} – \cos {x}\sin{y} \) = \( \sin {(x – y)} \) = 0 Therefore, we have x – y = nπ where n ∈ Z ⇒ x = nπ y Example 3 Find the solution of \( \sin {x} \) = \( \frac {\sqrt {3}}{2} \)In this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometric
Math\sin^2x\cos^2x=1/math math\implies\dfrac{\sin^2x}{\cos^2x}\dfrac{\cos^2x}{\cos^2x}=\dfrac{1}{\cos^2x}/math math\implies\left(\dfrac{\sin x}{\cos x1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go! · Proving the trigonometric identity $(\tan{^2x}1)(\cos{^2(x)}1)=\tan{^2x}$ has been quite the challenge I have so far attempted using simply the basic trigonometric identities based on the Pythagorean Theorem I am unsure if these basic identities are unsuitable for the situation or if I am not looking at the right angle to tackle this problem trigonometry Share Cite



Solved Proving Trigonometric Identities Q1 Prove That Sin Chegg Com
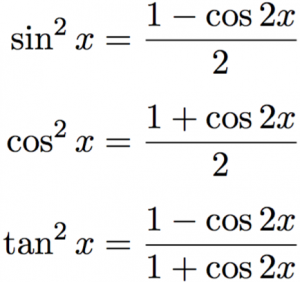


Trig Identities Table Of Trigonometric Identities
The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies The Greeks focused on the calculation of chords, while mathematicians in India created the earliestknown tables of values for trigonometric ratios (also called trigonometric functions) such as sineCsc^2xtan^2x 1=tan^2x Verifying Trigonometric Identities, How to Verify Trig Identities Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, tryTrigonometric Integrals In this section we use trigonometric identities to integrate certain combinations of trigonometric functions We start with powers of sine and cosine EXAMPLE 1 Evaluate SOLUTION Simply substituting isn't helpful, since then In order to integrate powers of cosine, we would need an extra factor Similarly, a power of sine would require an extra factor



Trig Identities Bingo Card
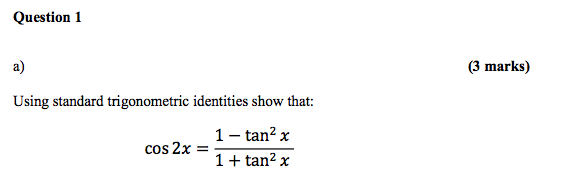


Solved A Using Standard Trigonometric Identities Show Th Chegg Com
LS = (sec^2 x tan^2 x), and it equals the right sideFree trigonometric identities list trigonometric identities by request stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing Practice;We rearrange the trig identity for sin 2 2x We divide throughout by cos 2 2x The LHS becomes tan 2 2x, which is our integration problem, and can be expressed in a different form shown on the RHS However, we still need to make some changes to the first term on the RHS We recall a standard trig identity with secx This is usually found in formula books We square both sides,


Answered O Trigonometric Identities And Bartleby



Solved Inquiry 11 8 Marks Prove The Following Trig Ide Chegg Com
· more tan²θ = sin²θ cos²θ = 1 That is wrong tan²θ = sin²θ/cos²θ Secondly, the identity is tan²θ 1 = sec²θ, not tan²θ 1 Maybe this proof will be easier to follow tan²θ 1 = sin²θ/cos²θ 1 = sin²θ/cos²θ cos²θ/cos²θ = (sin²θ cos²θ)/cos²θ //sin²θ · Using some trigidentities we have $$\tan(2x)=\frac{2\tan(x)}{1\tan^2(x)}$$ and $$\cos(2x)=2\cos^2(x)1$$ and $$\tan^2(x)=\sec^2(x)1$$ we have (on the left hand side) $$\begin{align}\tan(2x)\tan(x)&=\frac{2\tan(x)}{1\tan^2(x)}\tan(x)\\&=\frac{2\tan(x)\tan(x)\tan^3(x)}{1\tan^2(x)}\\&=\tan(x)\frac{1\tan^2(x)}{1Trig identity $1\tan x \tan 2x = \sec 2x$ Ask Question Asked 9 years, 11 months ago Active 5 years, 9 months ago Viewed 6k times 3 0 $\begingroup$ I need to prove that $$1\tan x \tan 2x = \sec 2x$$ I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong



Solved 17 Prove The Following Trig Identities Tan 2x Chegg Com



Math34 Trigonometric Formulas
Therefore in mathematics as well as in physics, such formulae are useful for deriving many important identities The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula isSimplify trigonometric expressions Calculator online with solution and steps Detailed step by step solutions to your Simplify trigonometric expressions problems online with our math solver and calculator Solved exercises of Simplify trigonometric expressionsTrigonometric Identities mcTYtrigids091 In this unit we are going to look at trigonometric identities and how to use them to solve trigonometric equations In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature After reading this text, and/or viewing the video tutorial on this topic, you should be



Double Angle Identities Solutions Examples Videos Worksheets Games Activities



Trig Double Identities Trigonometric Double Angle Functions Trig
Summary Calculator wich uses trigonometric formula to simplify trigonometric expression trig_calculator online Description This calculator allows through various trigonometric formula to calculate trigonometric expressionTrignometric expressions are expressions that involve sine functions, cosine functions , tangent functionProving Trigonometric Identities Calculator Get detailed solutions to your math problems with our Proving Trigonometric Identities stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here! · 1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2x Trigonometry Science



Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity



Solved Using Standard Trigonometric Identities Show That Chegg Com
· Prove trig expression Transform the left side of the expression LS = sec^4 x tan^4 x = (sec^2 x tan^2 x)(sec^2 x tan^2 x) Since the first factor, (sec^2 x tan^2 x) = (1/(cos^2 x) (sin^2 x)/(cos^2 x)) = = (1 sin^2 x)/(cos^2 x) = (cos^2 x)/(cos^2 x) = 1 There for, the left side becomes;Trigonometricidentitycalculator Prove (sec^{4}x sec^{2}x) = (tan^{4}x tan^{2}x) en · 71 Solving Trigonometric Equations with Identities In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions



Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube


Trig Identities Hsn Forum
The Trigonometric Double Angle identities or Trig Double identities actually deals with the double angle of the trigonometric functions For instance, Sin2(α) Cos2(α) Tan2(α) Cosine2(α) Sec2(α) Cot2(α) Double Angle identities are a special case of trig identities where the double angle is obtained by adding 2 different angles In this article, we will cover upIn this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometric · sin^2xsin^2xtan^2x=tan^2x Simplify sin^2xsin^2xtan^2x First, factor out sin^2x from the expression sin^2x(1tan^2x) Now we can use this trig identity 1tan^2x=sec^2x Now we have sin^2xsec^2x We know that secx=1/cosx So it is then true that sec^2x=1/cos^2x Now we have sin^2x/cos^2x We know that tanx=sinx/cosx So it is then true that tan^2x=sin^2x/cos^2x So for



Solved 2 Prove The Following Trig Identities A Prove Chegg Com



Magic Hexagon For Trig Identities
Question I need to prove this identity tan^2xsin^2x = tan^2xsin^2x Answer by lwsshak3() (Show Source) You can put this solution on YOUR website!Account Details Login Options Account Management SettingsBecause the two sides have been shown to be equivalent, the equation is an identity tan(2x) cot(2x) csc(2x) = sec(2x) tan (2 x) cot (2 x) csc (2 x) = sec (2 x) is an identity


What Is The Formula Of Tan2x Quora



2sinxcosx Identity Gamers Smart
Trigonometric identity example proof involving all the six ratios Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organizationIn mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right triangles There are loads of trigonometric identities, but the following are the ones you're most likely toTrig Cheat Sheet Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p


Trig Identities Crossword Wordmint
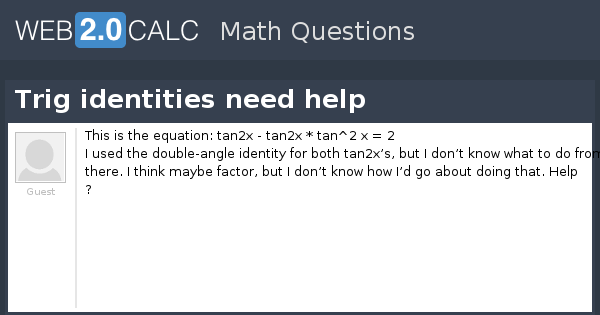


View Question Trig Identities Need Help
Basic Identities \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos (x)} {\sin (x)} \sec (x) = \frac {1} {\cos (x)} \csc (x) = \frac {1} {\sin (x)}2321 · \(\tan ^2x=\dfrac{1−\cos 2x}{1\cos 2x}\) Power reducing identities are most useful when you are asked to rewrite expressions such as \sin 4x as an expression without powers greater than one While \(\sin x\cdot \sin x\cdot \sin x\cdot \sin x\) does technically simplify this expression as necessary, you should try to get the terms to sum together not multiply togetherExamples prove\\tan^2 (x)\sin^2 (x)=\tan^2 (x)\sin^2 (x) prove\\cot (2x)=\frac {1\tan^2 (x)} {2\tan (x)} prove\\csc (2x)=\frac {\sec (x)} {2\sin (x)} prove\\frac


Biomath Trigonometric Functions



Lesson 4 5 Double Angle Formulas
Notebook Groups Cheat Sheets;The trig inequality tan 2x sin x – cos 2x > 2 has 2Pi as common period The trig inequality tan x cos x/2 < 3 has 4Pi as common period Unless specified, a trig inequality must be solved, at least, within one whole common periodIn trigonometry, quotient identities refer to trig identities that are divided by each other There are two quotient identities that are crucial for solving problems dealing with trigs, those being for tangent and cotangent Cotangent, if you're unfamiliar with it, is the inverse or reciprocal identity of tangent This identity will be more clear in the next section Below, this image covers



Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube
· All trigonometric identities are cyclic in nature They repeat themselves after this periodicity constant This periodicity constant is different for different trigonometric identities tan 45° = tan 225° but this is true for cos 45° and cos 225° Refer to the above trigonometry table to verify the valuesAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsTrigonometric Identities and Formulas Below are some of the most important definitions, identities and formulas in trigonometry Trigonometric Functions of Acute Angles sin X = opp / hyp = a / c , csc X = hyp / opp = c / a tan X = opp / adj = a / b , cot X = adj / opp = b / a cos X = adj / hyp = b / c , sec X = hyp / adj = c / b , Trigonometric Functions of Arbitrary Angles sin X = b / r



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
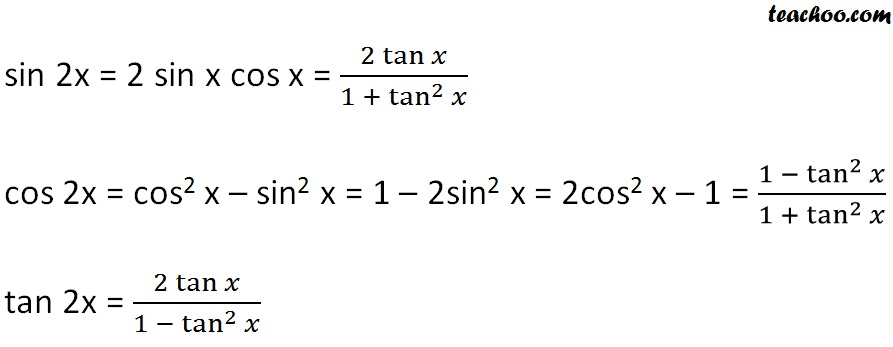


Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
Some simple trigonometric equations 2 4 Using identities in the solution of equations 8 5 Some examples where the interval is given in radians 10 wwwmathcentreacuk 1 c mathcentre 09 1 Introduction This unit looks at the solution of trigonometric equations In order to solve these equations we shall make extensive use of the graphs of the functions sine, cosine and tangent



Solved 5 2 Verify The Following Trigonometric Identities Chegg Com



Trigonometry Reciprocal Identities Expii



Xswjl Vrk4qd7m



Trig Identities Crossword Wordmint



How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic



Trig Integrals Trig Substitution


Trig Identities Hsn Forum


7 Proving Ids Trig Functions Identities
.JPG)


Every Day I M Calculatin I D3 Unit Q Pythagorean Identities


Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero


Answered O Trigonometric Identities And Bartleby



How To Prove Quotient And Reciprocal Identities Studypug



Verify Each Trigonometric Equation By Substituting Identities To Match The Right Hand Side Of The Brainly Com



Solved 2 Prove The Following Trig Identities A Prove Chegg Com



How To Prove Derive Trigonometric Identities Video Lesson Transcript Study Com



Trigonometric Identities And Examples With Worksheets



How Do You Prove Tan 2x Secx 1 1 Secx Socratic


Math Problems Simplifying With Trigonometry Identities And Then Integration



Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube



Using Trigonometric Identities Video Khan Academy



Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
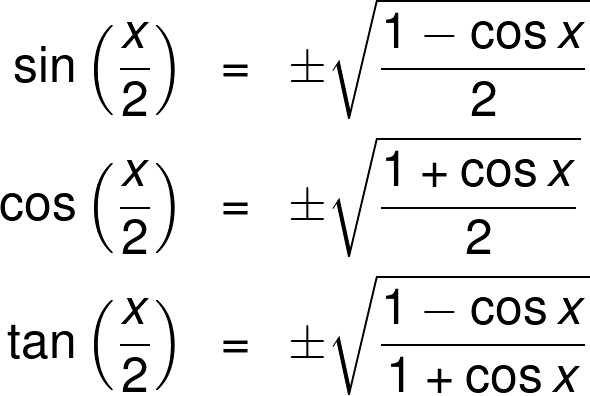


Half Angle Calculator



14 2 Trigonometric Identities



Trigonometric Identities Learn Trigonometry By Ib Elite Tutor



Chapter 11 Trigonometric Identities And Equations 11 1


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities


What Is The Formula Of Tan2x Quora



How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic


What Is The Formula Of Tan2x Quora



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Integrate Sec 2x Method 1
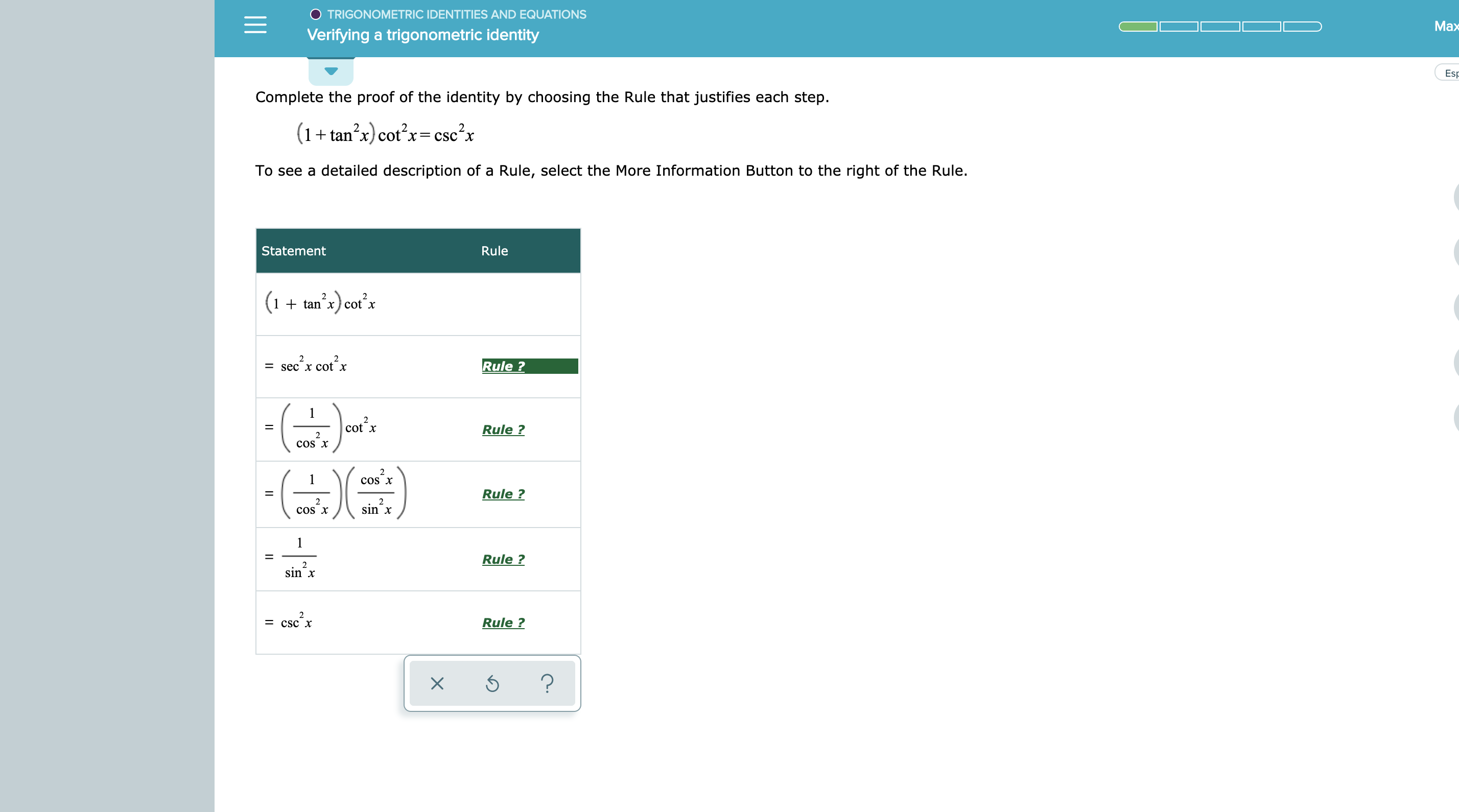


Answered Trigonometric Identities And Equations Bartleby



Which Of The Following Is Not An Identity A Cosx Sinx 2 1 2cosx Sinx B 1 Cos 2x Sin 2 1 Brainly Com



Weierstrass Substitution Wikipedia


Biomath Trigonometric Functions



How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube



9 1 Identities And Proofs Ppt Download



14 2 Trigonometric Identities


Trigonometric Identities Cheat Sheet Doubleroot In



1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube



Trig Identities Maple Learn Maplesoft


How Can One Prove That Math Tan 2x 2 Cot X Tan 2x Cot 2 X Math Quora



Ch 7 Trigonometric Identities And Equations Ppt Video Online Download



Trig Identities Bingo Card



Trig Angle Addition Identities Video Khan Academy



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions



Tan 2x Identity Learn Lif Co Id


View Question For Questions 1 5 Decide Whether The Equation Is A Trigonometric Identity Explain Your Reasoning



Tangent Half Angle Formula Wikipedia



How To Use Trig Identities Mathematics Stack Exchange



Trig Identities And Formulas Pre Calculus Quiz Quizizz
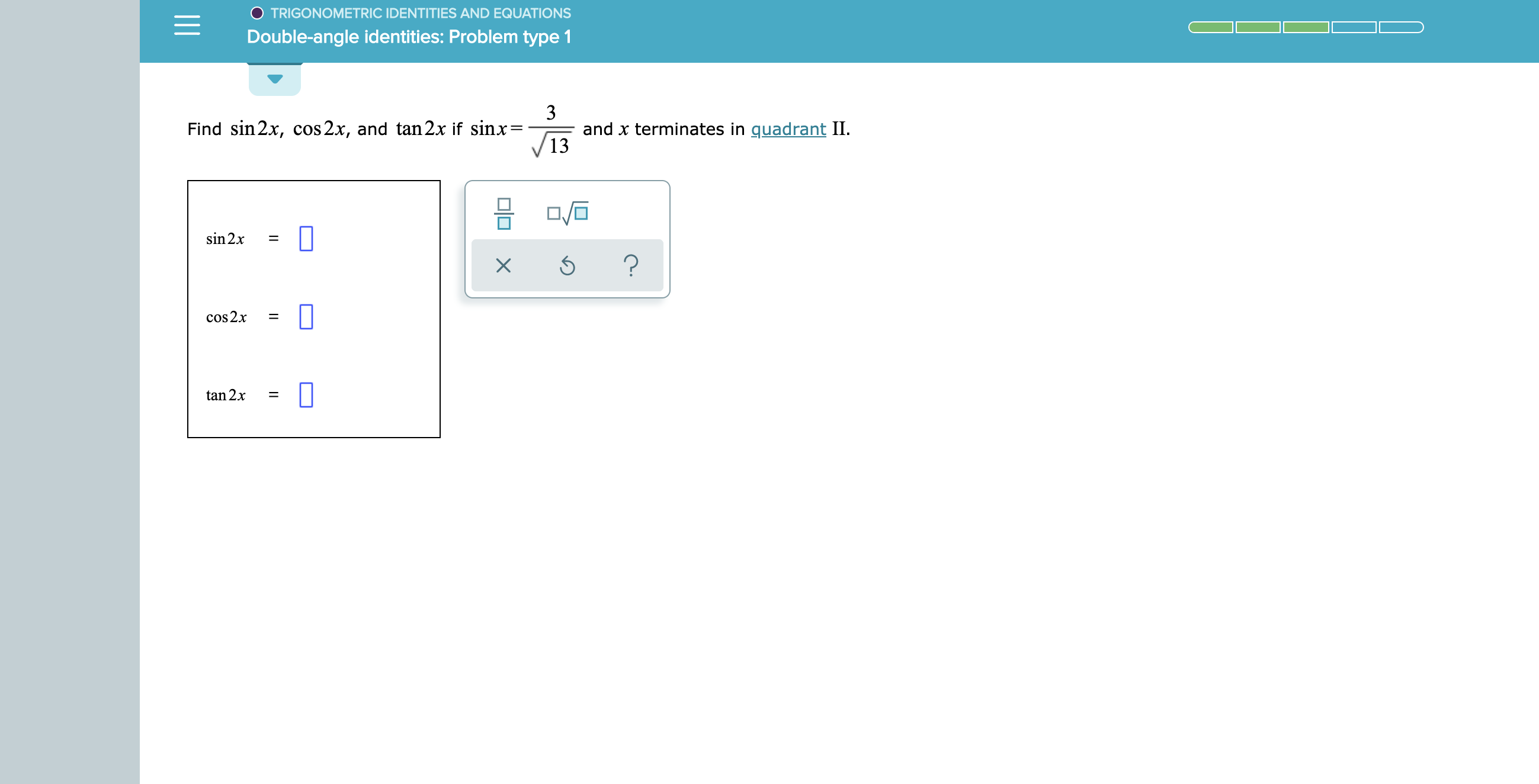


Answered Trigonometric Identities And Equations Bartleby


6 1 2 Trigonometric Identities
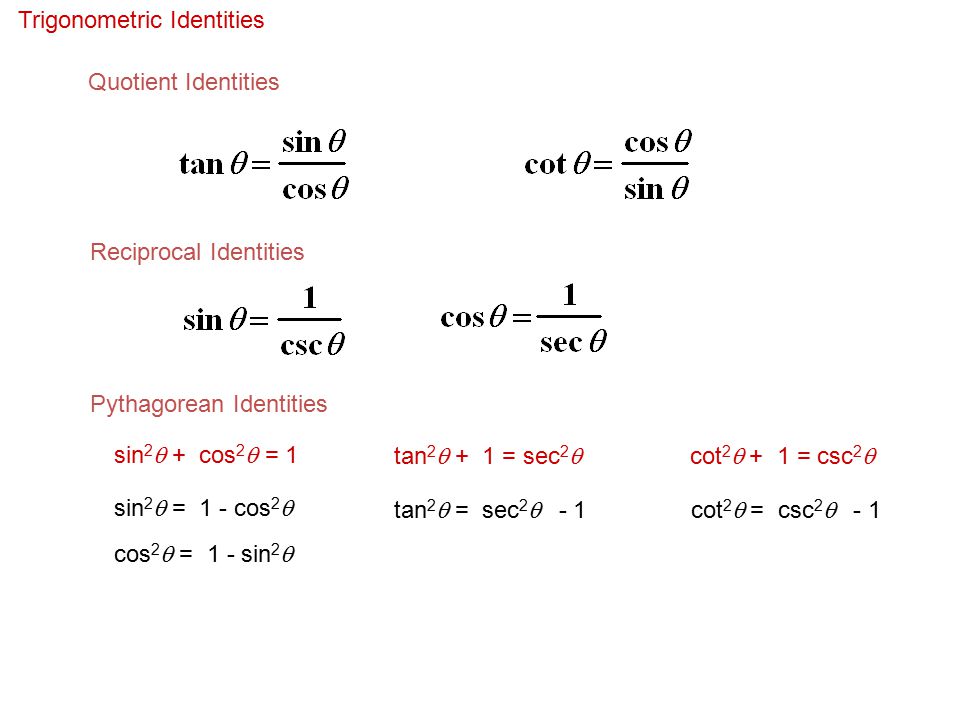


11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



Sum And Difference Identities Video Lessons Examples And Solutions


Ilectureonline


Derivatives Of Trigonometric Functions



Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube


A Trig Identity



Integrate Tan 2x


What Is The Formula Of Tan2x Quora



Trig Identity Sec2x Minus Tan2x T10 Youtube



Tan 2x Identity Learn Lif Co Id



List Of Trigonometric Identities Wikipedia



Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
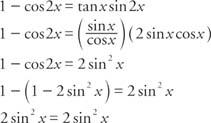


Double Angle And Half Angle Identities



How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic


