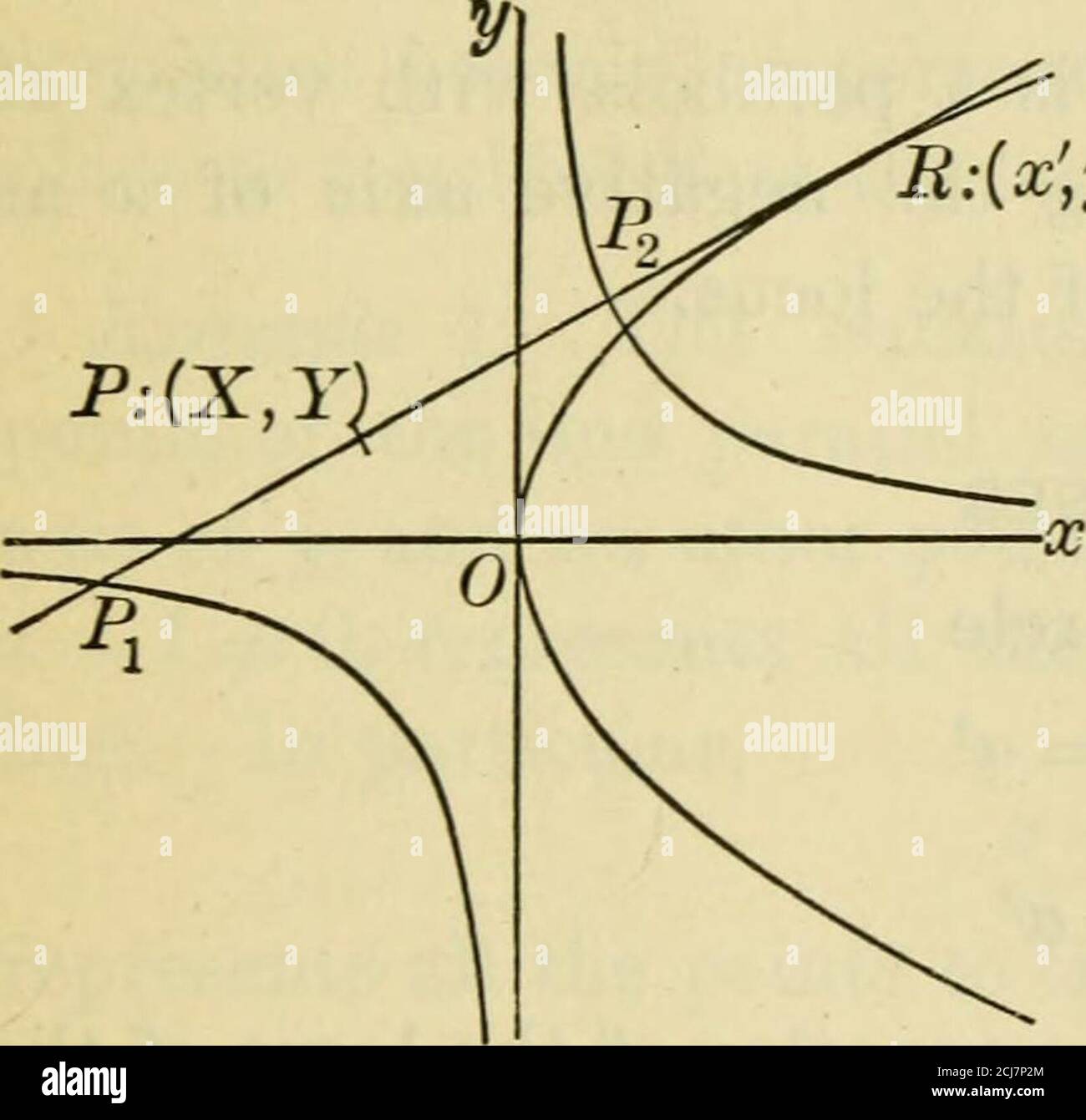
X^2(y2)^2=4The boundaries of the segment are defined by the equations x2 y2 = 4, xy −2 = 0 Solution The circle x2 y2 = 4 has the radius 2 and centre at the origin (Figure 4 ) Figure 4 Since the upper half of the circle is equivalent to y = √4− x2, the double integral can be written in the following form ∬ R x2ydxdy = 2 ∫ 0 √4− water flows out in 7 minutes Initially the tank isfilled with 8000 liters of water Find the amount of water left after21 minutes for what value of k, x= 2^y=2/3 is a solution of 2x3y=k 2 CalculateADC ()ABC ВАСB130EСD I am boorred can anyone inboxx mee 63x25=I want the equation Code Google meet cyjpxsqgtijoin fasthaveFind and sketch the domain of the function of f(x;y) = p x2 y2 The inside of a square root must be nonnegative So f(x;y) is defined only if x2 y2 0 In other words, the domain is x2 y2 0 Note that x2 y2 = (x y)(x y) = 0 Therefore the boundary is the union of two diagonal lines passing through the origin
1
(x y)^3-(x-y)^3-6y(x^2-y^2)=ky^2
(x y)^3-(x-y)^3-6y(x^2-y^2)=ky^2-4x 9y 3 (xy) First, we will start by opening the bracket, so the expression becomes; Example If the lines 2x y – 3 = 0, 5x ky – 3 = 0 and 3x – y – 2 = 0 are concurrent, find the value of k Three lines are concurrent if they pass through a common point ie point of intersection of any two lines lies on the third line It is given that lines 2x y − 3 = 0 5x



2
x 2 2y 3 1 x y 3 3 Mathematics TopperLearningcom gl2kl500 The graphs of the lines 3x 4y = 2, 5x y = 11 and x ky = 2 all contain the same point asked in ALGEBRA 2 by chrisgirl Apprentice systemofequationsbygraphingSolution satisfies φ(x,y) = x2y2 2xy = C 3 (Sec 26 Problem 16) Determine the value of b such that the following equation is exact, and then solve the equation (ye2xyx)dxbxe2xydy = 0 Solution Let M(x,y) = ye2xy x and N(x,y) = bxe2xy We have M y = e2xy 2xye 2xyand N x = be 2bxye2xy So M y = N x if b = 1 Thus there is a function
SolutionShow Solution The given equation is (x y) 3 − (x − y) 3 − 6y (x 2 − y 2) = ky 2 Recall the formula `a^3 b^3 = (ab) (a^2 ab b^2)` Using the above formula, we have ` (xy)^3 (xy)^3 6y (x^2 y^2 )ky^2` `⇒ { (xy)^3 (xy)^3} 6y (x^2 y^2) = ky^2`EC02 Spring 06 HW9 Solutions 3 y=x w/2 xy=1 X 1 w w−x 1 Y x x To distinguish between the random variables and their values, I have been careful here to use capital letters for the random variable names and lower case letters for the specific values they takeAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}yxy^ {2}=4 x 2 y x y 2 = 4 Subtract 4 from both sides of the equationSteps for Solving Linear Equation ( 2 x y ^ { 2 } 3 ) d x ( 2 x ^ { 2 } y 4 ) d y = 0 (2xy2 − 3)dx (2x2y 4)dy
Solution 1 First assume y 2 =ux 2, and y 2 '=2uxu'x 2 and y 2 ''=u''x 2 4u'x2u Substituting into x 2 y''2xy'6y=0 we get x 2 (u''x 2 4u'x2u)2x(2uxu'x 2)6y=0 and simplifying by adding like terms we get u''x 4 6u'x 3 =0 We reduce the order by w=u' to get w'x 4 6wx 3 =0 Now dividing by wx 4 and rearranging, we get and integrating bothSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreView Task7 Calc3docx from MATH C657 at Western Governors University Given the multivariable function of f(x,y) = ky 2 – 2y 3 – kx 3 2kxy, we can show that there is a saddle point at (0,0)




Which Of The Following Pairs Of Linear Equations Are Consistent Inconsistent If Consistent Obtain The Solution Graphically I X Y 5 2x 2y 10 Ii X Y 8



2
2(5) 3y = 16 10 3y = 16 3y = 6 y = 2 So our solution is (5,2) or ELIMINATION METHOD xy =3 2x3y=16 I'm going to eliminate the y Multiply the top equation by 3 3(xy = 3) 2x3y = 16Simplify 3x3y=9 2x3y=16 Add the two equations together 5x 0y = 25 x = 5 Then substitute x=5 back into one of the original equations, let's use the Show activity on this post Your method can't find two other critical points You successfully found that x y = ± 6 and x − y = ± 2, but plus and minus signs don't need to coincide Then four possibilities occur x = 6 2 2 x = 6 − 2 2 x = − 6 2 2 x = − 6 − 2 2 Here 2 and 3 are missing in your attempt যদি (xy)^(3)(xy)^(3)6y(x^(2)y^(2))=ky^(2) , তারপরে কে = Updated On 23 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y



2
X^3 x^2 y x y^2 y^3 Natural Language;Let y=0 and solve for x, this is your xintercept 3x3 (0)=6 3x=6 3x/3=6/3 x=2 Plot (2,0) Notice that is the same xintercept that L1 had L1 is lying right ontop of L2, in other words they graphically are the same line The solution is all real numbersLeast common multiple of 3 and 5 is 15 Multiply \frac {2xy} {3} times \frac {5} {5} Multiply \frac {3x2y} {5} times \frac {3} {3} To add or subtract expressions, expand them to make their denominators the same Least common multiple of 3 and 5 is 1 5 Multiply 3 2 x y times 5 5 Multiply 5 3 x − 2 y times 3 3 Since \frac {5\left (2x



2



Bookidplanesolidan High Resolution Stock Photography And Images Alamy
Facebook Whatsapp Transcript Ex 63, 11 Solve the following system of inequalities graphically 2x y ≥ 4, x y ≤ 3, 2x – 3y ≤ 6 First we solve 2x y ≥ 4 Lets first draw graph of 2x y = 4 Putting x = 0 in (1) 2 (0) y = 4 0 y = 4 y = 4 Putting y = 0 in (1) 2x (0) = 4 2x = 4 x = 4/2 x = 2 Points to be plotted are (0, 4), (22 3\pi e x^{\square} 0 \bold{=} Go Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Apply the product rule to 3 x 2 3 x 2 Raise 3 3 to the power of 3 3 Multiply the exponents in (x2)3 ( x 2) 3 Tap for more steps Apply the power rule and multiply exponents, ( a m) n = a m n ( a m) n = a m n Multiply 2 2 by 3 3 Multiply the exponents in (y3)3 ( y 3) 3




3 Find The Solution To Y 6y 8y 16 X 0 0 X 0 0 Given That Y X Ce Cze Homeworklib



If X Y X Y 6y X Y Ky What Is K Quora
3 X Y x=y2 y=x2 (1,1) (4,2) Figure 2 The area between x = y2 and y = x − 2 split into two subregions If we slice the region between the two curves this way, we need to consider two different regions Where x > 1, the region's lower bound is the straight line For x < 1, however, the region's lower bound is the lower half of the The inequalities are 2x 3y ≥ 6, x y ≥ 3 and y ≤ 2 Rewrite the inequalities so that solves for y , That's the slope intercept form and it will make the boundary line easier to graph 1) Draw the coordinate plane The first inequality 2x 3y ≥ 6 3y ≥ 2x 6 y ≥ ( 2/3)x 2 2) Graph the line y = ( 2/3)x 2 3) Since the inequality symbol is ≥ the boundary isX y m n 306 19 35 1 300 13 37 13 297 80 19 8 290 171 39 19 286 279 35 9 285 92 17 2 275 42 18 7 273 232 17 4 270 119 37 17 261 2 19 10 260 1 33 7 255 38 16 1 253 12 17 6 247 150 16 3 240 17 31 1 234 115 31 5 230 39 33 13 225 112 17 8 221 84 15 2 216 9 35 19 210 11 31 11 8 57 29 3 7 70 16 7 0 153 33 17 198 175 29 7 195



1
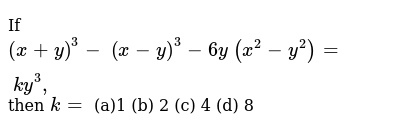



If X Y 3 X Y 3 6y X 2 Y 2 K Y 3 Then K A 1 B 2 C 4 D 8
If xy^3xy^36yx^2y^2=ky^2 find k x y³ x y³ If (xy)^3(xy)^36y(x^2y^2)=ky^2, find k Please scroll down to see the correct answer and solution guideFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorSolution for 2xy6xy3=0 equation Simplifying 2xy 6x y 3 = 0 Reorder the terms 3 6x 2xy y = 0 Solving 3 6x 2xy y = 0 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right




Engineering Mathematics Notes



2
The calculator will try to find the solution of the given ODE firstorder, secondorder, nthorder, separable, linear, exact, Bernoulli, homogeneous, or inhomogeneous Initial conditions are also supported Your input solve $$$ y ' \left (x \right) = x^ {2} $$$X^3 3x^2y 3xy^2y^3 (x y)^3 Solution Well you can use many methods to simplify like Using Pascal Triangle which give be 1, 3, 3, 1 as the expansion You can simplify (x y)^3 to either (x y) (x y) (x y) or (x y)^2 (x y) But using those two will result in sameIf the system of equations 2x 3y – z = 0, x ky 2z = 0 and 2x – y z = 0 has a nontrivial solution (x, y, z), then \(\frac{x}{y} \frac{y}{z} \frac{z}



Files Eric Ed Gov




Simplify X Y 3 X Y 3 6y X 2 Y 2 Youtube
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Find the equations of the tangents from the point A(3,2) to the circle x^(2)y^(2)4x6y8=0Class12Subject MATHSChapter CIRCLE BookARIHANT MATHSBoardII You have an Implicit Function in which y is function of x so you have to derive it as well You get (1 ⋅ y2 2xy dy dx) − (3x2y x3 dy dx) = 0 using the Product Rule Then y2 2xy dy dx − 3x2y −x3 dy dx = 0 Collecting dy dx dy dx 2xy − x3 = 3x2y −y2 dy dx = y(3x2 − y) x(2y − x2) Hope it helps



Graph Xy3



X Y 3 X Y 3 Can Be Factorized As A 2y 3x 2 Y 2 Sarthaks Econnect Largest Online Education Community
Click here👆to get an answer to your question ️ If (x y)^3 (x y)^3 6y(x^2 y^2) = ky^2 , then k =Get an answer for '2x 3y = 2 x 3y = 7 find x and y' and find homework help for other Math questions at eNotesSimple and best practice solution for 3(x2)=y6 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,



2



2
Answer (1 of 9) After Solving the equation x = y or x = y so yy =0 ans is ZERO or 2*y(2 x) dy dx = 3y This is a First Order separable Differential equation, and we can rearrange as follows 1 y dy dx = 3 x 2 And we can "separate the variables" to get ∫ 1 y dy = ∫ 3 x 2 dx If the linear equation in two variables 2x –y = 2, 3y –4x = 2and px–3y = 2are concurrent, then find the value of p If ܽa b = 35 and a − b =




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr



X Y Graph
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicStart your free trial In partnership with You are being redirected to Course Hero I want toAny tangent to y2 = 4x is y = mx 1m It touches the circle, if 3 = 3m 1m1 m2⇒ 91 m2 = 3m 1m2⇒ 91 m2m2 = 3m2 12⇒ 9m2 9m4 = 9m4 1 6m2⇒ 3m2 = 1⇒ m = ± 13For the common tangent to the above xaxis we takem = 13∴ Equation of common tangent is, y = x3 3⇒ 3y = x 3



X Y 3 Graph




Engineering Mathematics Notes
Easy as pi (e) Unlock StepbyStep (x^2y^21)^3x^2y^3=0 Natural Language Math Input NEW Use textbook math notation to enter your mathWatch Video in App This browser does not support the video element 348 k 17 k AnswerAnswer (1 of 2) 3/x2/y=0 take lcm or multiply both lhs and rhs with xy 3y2x=0 3y=2x substitute 3y=2x in the other equation 2/x2/(2x)=1/6 2/x1/x=1/6 as they are like fractions we can perform subtraction 1/x=1/6 therefore x=6 and substituting x=6 in any eqn find the value of y




If X Y 3 X Y 3 6y X 2 Y 2 K Y 3 Then K A 1 B 2 C 4 D 8
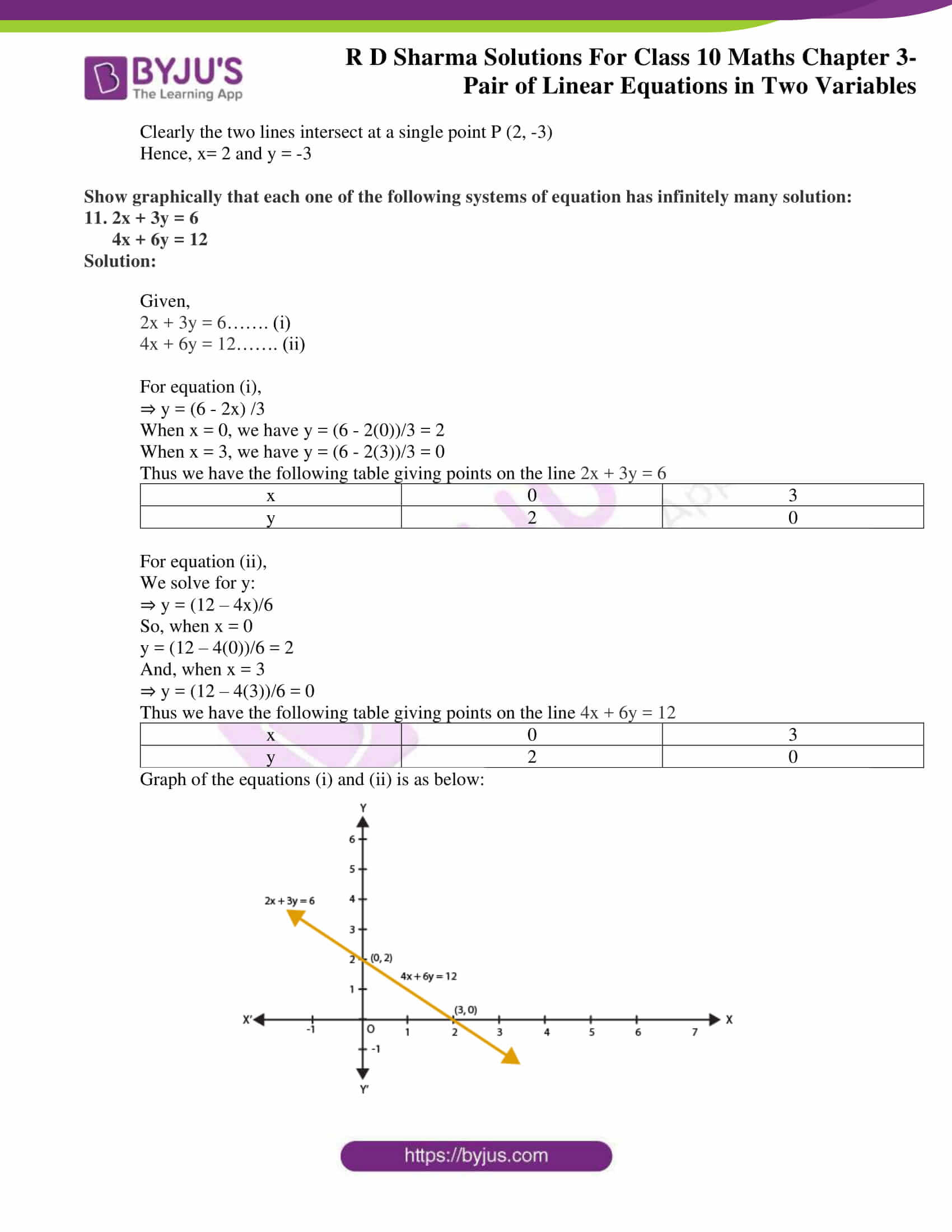



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
We will use the elimination method to solve First, multiply (2) by 2 and add to (1) 7y = 2 ==> y= 2/7 Now substitute y= 2/7 in (2) x 2y= 3 x 2 (2/7) = 3 x 4/7= 3 Move 4/7 to the When y = 1, then x = 3 When y = 5, then x = 4 Hence, the two solutions are (3, 1) and (4, 5) Question 2 The path of an aeroplane is given by the equation 3x – 4y = 1 2 Represent the path graphically Also, show that the point (4,6) lies on the graph Solution Given equation is 3x – 4y = 12 ∴ y = \(\frac{3 x12}{4}\) When x = 0




Simplify X Y X Y 6y X Y Brainly In



Cambridge Org




If X Y 3 X Y 3 6y X 2 Y 2 K Y 3 Then K A 1 B 2 C 4 D 8



Hubei Gov Cn
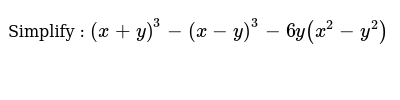



Simplify X Y 3 X Y 3 6y X 2 Y 2
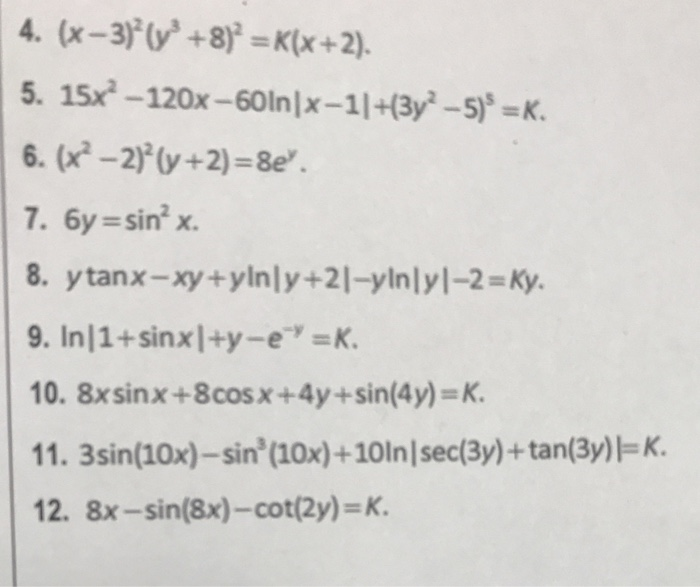



Solved 4 Solve The De X Y 8 Dx 6 X X 6ly Dy 5 Solve The Chegg Com



Journals Sagepub Com




Ch 1 2




Example If Lines 2x Y 3 0 5x Ky 3 0 Concurrent




If X And Y Are Positive Integers Which Of The Following Problem Solving Ps




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy




Solved Find All The Local Maxima Local Minima And Saddle Chegg Com




If X Y 3 X Y 3 6y X 2 Y 2 K Y 2 Then K A 1 B 2 C 4 D 8 Youtube




Sol Purcell Ingles



The Value Of K For Which The System Of Equations Kx Y 2 And 6x 2y 3 Has A Unique Solution Is What Mathematics Topperlearning Com 6dworn




Simplify X Y 3 X Y 3 6y X 2 Y 2 Youtube
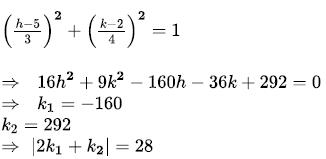



If The Equation Of The Curve On Reflection Of The Ellipse About The Linex Minus Y Minus 2 0is16x2 6y2 K1x Minus 36y K2 0 Then Find The Value Of 2k1 K2 2k1 K2 Correct Answer Is 28 Can You Explain This Answer Edurev Jee Question




Pdf On The Diophantine Equation X 2 Kxy Y 2 Lx 0
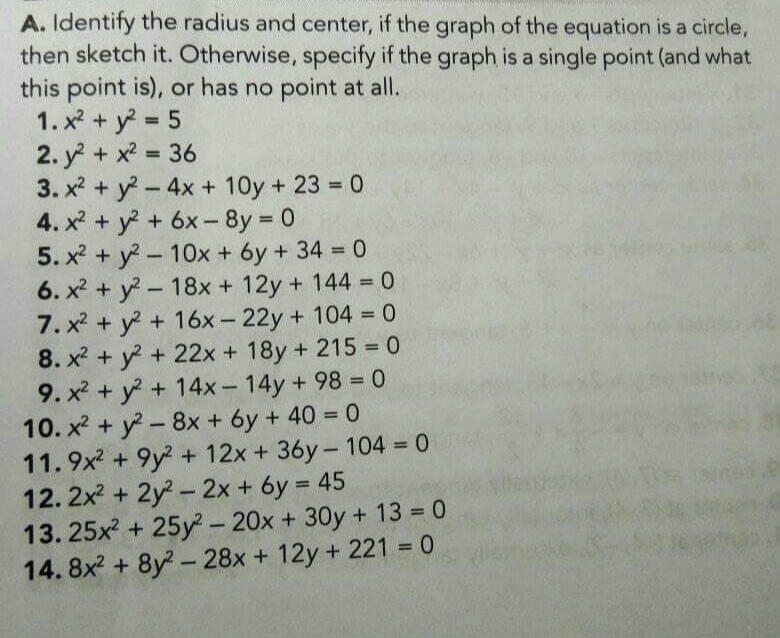



Answered 10 X Y 8x 6y 40 0 11 9x 9y Bartleby




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Brainly In



2




Exact Exact Exact Pdf




Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 5 Avail Free Pdf




Ncert Exemplar Class 10 Maths Solutions Chapter 3 Pair Of Linear Equations In Two Variables Cbse Tuts




3 Given X Y X Y 6y X2 Y2 Ky Then The Value Of K Is Brainly In



Tensors And Multilinearity Springerlink




Example 40 If Y 3e2x 2e3x Prove D2y Dx2 5 Dy Dx



Bookidplanesolidan High Resolution Stock Photography And Images Alamy



2




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y



2



2




Simplify X Y 3 X Y 3 6y X 2 Y 2




Solve 2xy X Y 3 2 Xy 2x Y 3 10 Mathematics Topperlearning Com X2oivz99



2




Problem Sets 5 With Prof Edward Dowling Homework 5 Optimizing Functions Quadratic And Cubic Studocu



Parametric Equations For The Intersection Of Planes Krista King Math Online Math Tutor
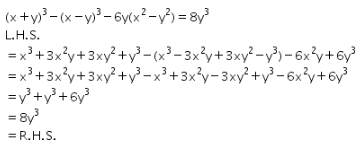



Prove That X Y 3 X Y 3 6y X2 Y2 8y3 Cbse Class 9 Maths Learn Cbse Forum



Cbse 8 Math Ncert Solutions



Simultaneous Equations Gmat Math Study Guide



Show Graphically That The System Of Equations X 2y 5 3x 6y 15 Has Infinitely Many Solutions Mathematics Shaalaa Com




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Mathematics Topperlearning Com Jd2kccrr




Engineering Mathematics Ii Ma Ppt Download




Engineering Mathematics Notes
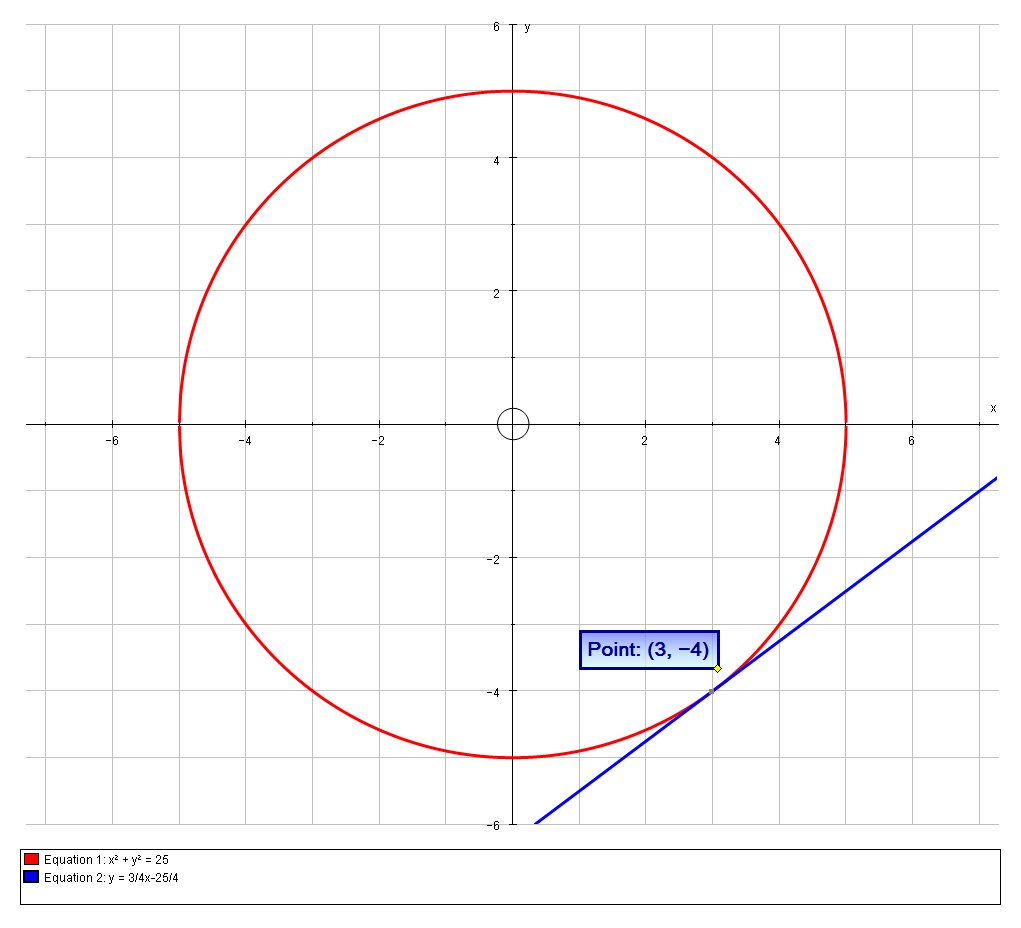



How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic
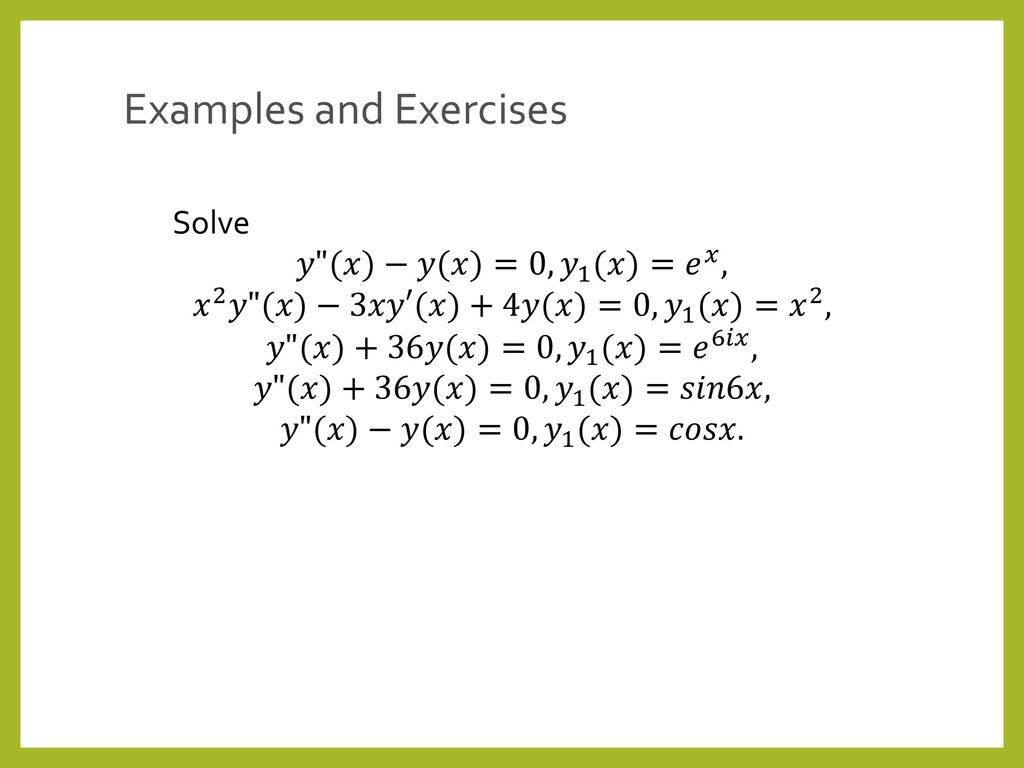



Engineering Mathematics Ii Ma Ppt Download
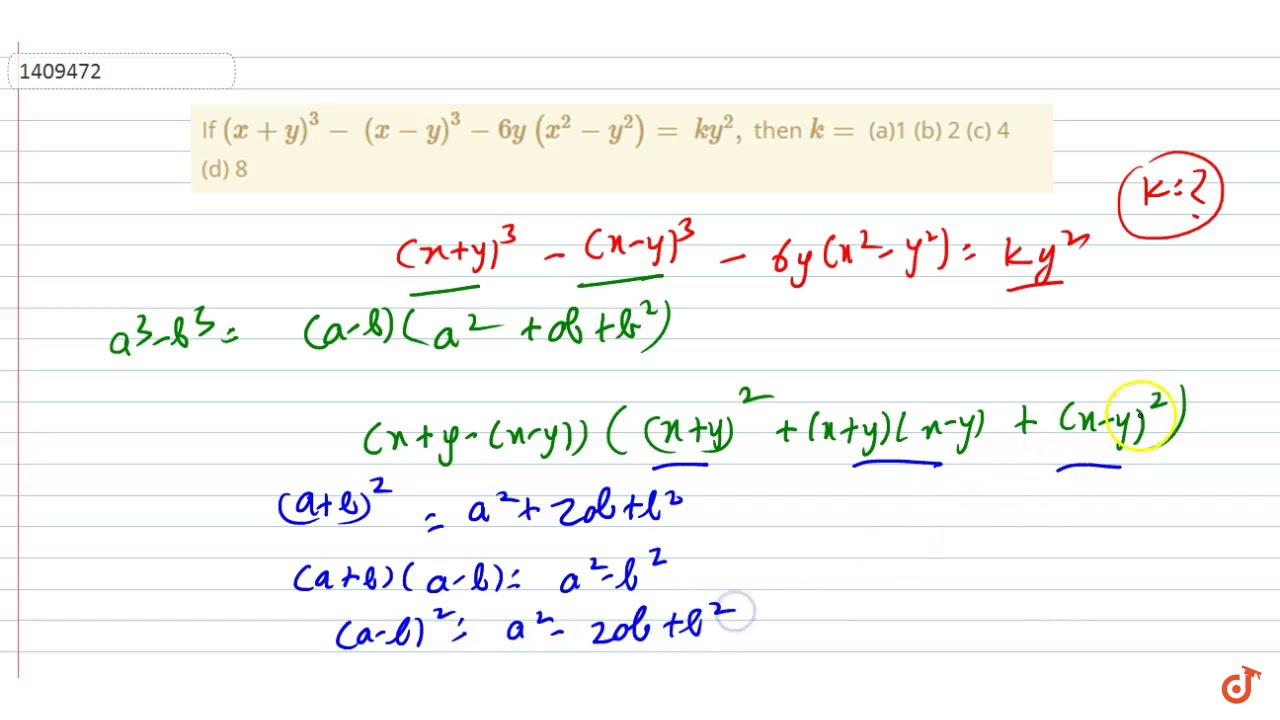



If X Y 3 X Y 3 6y X 2 Y 2 K Y 2 Then K A 1 B 2 C 4 D 8 Youtube




If 6xy X 2 Y 9y What Is The Value Of Xy Data Sufficiency Ds




Solved Fid Gcneral Solutions Of The Differential Equations In Prob Lens Through 30 Prinies Denote Derivatives Mith Ruprct 0 X Thrughou 1 Wy 2 Zxyy 2y J Vv Y Y 5 6 Wy Yu Y



2



2




Lecture Notes 3 Pdf




Solving A System Of Equations Using A Matrix Precalculus Socratic




For What Value Of K The Pair Of Linear Equations 3x Y 3 And 6x Ky 8



If X Y X Y 6y X Y Ky What Is K Quora




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y




Maxima And Minima



2



2



How Can One Find The Values Of K For Which The Line 2x K Is Tangent To The Circle With The Equation X 2 Y 2 5 Quora
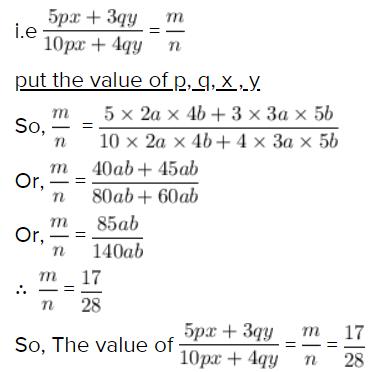



Test Ratio And Proportion Indices Logarithms 1 40 Questions Mcq Test



Jstor Org




Solved Homework Problems For Handout Sheet 10 1 Solve The De 3x Y Dx Xydy 0 2 Solve The De Y 8x Dx 8xy Dy 0 3 Solve The De 6y Xy Y Dx 2xdy 0 4 Solve The De Xydx X 3 Dy 0 5 Solve The




Glencoe Solution Manual




If The Angle Between Two Lines Represented By 2x 2 5xy 3y 2 7y 4 0 Is Tan 1m Then M Is Equal To




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Brainly In



2



Etd Ohiolink Edu



2



Systems Of Linear Equations
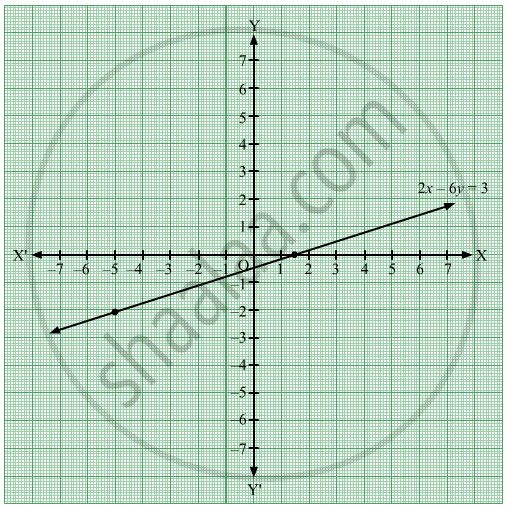



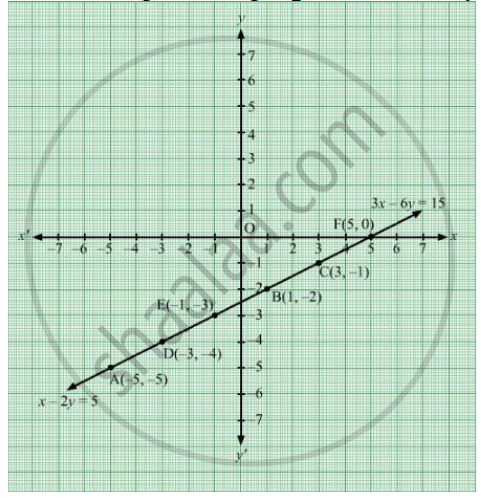
Complete The Following Table To Draw The Graph Of 2x 6y 3 Algebra Shaalaa Com




Assignment Previewer



If X Y 3 X Y 3 6y X 2 Y 2 Ky 2 Then K A 1 Sarthaks Econnect Largest Online Education Community



2




Simplify X Y 3 X Y 3 6y X 2 Y 2



2




Exact Equations Example 3 Video Khan Academy



Apps Dtic Mil




Mcq Questions For Class 10 Maths Pair Of Linear Equations In Two Variables With Answers Ncert Books



2


